Visualised Parallel Distributed Genetic Programming Applied on Stock Market Prediction
Submitted in partial fulfilment of the requirements for the MSc Degree in Computing Science of The University of London and for the Diploma of Imperial College of Science, Technology and Medicine.
Introduction
Genetic Programming (GP), as an extension of genetic algorithms, has been demonstrated to be an effective problem solving tool for tackling complex optimization and machine learning problems. In GP programs are expressed as parse trees to be executed. This form of GP has been applied successfully to a number of difficult problems like automated design, pattern recognition, robot control, classification, and many other areas.
When applied to business environment, especially capital market, GP offers not merely an alternative but a much advanced solution for market prediction against GAs. Because GP is actually evolving “strategies”, not formula coefficients, to assist investment decisions. However, the process of stock market prediction requires high computational resources, e.g., large memory and search times. Thus a variety of algorithmic issues are being studied to design efficient GPs.
Distributed computing applications attempt to harness the computing resources over network, which are believed able to offer a great amount of computational power and increase the overall rate of resource utilization at large. This project tries to exploit the inherent parallelism of GP by creating an infrastructure necessary to support distributed information processing using existing Internet and hardware resources. Instead of evolving the entire population using a single processor, we present here a distributed genetic programming engine which maintains multiple independent subpopulations interacting asynchronously using a controlled coarse-grain topology. This allows not only a better exploration of the global search space, but also delays premature convergence by introducing, via migration, diversity from other demes.
GeneProfit

Built upon my MetaDGPEngine, GeneProfit is a commercial standard software package that automates all necessary tasks for stock market prediction and self-training. From its graphical interface, it allows user to create different investment preference sets for any chosen stock symbol. On behind, it maintains SQL database for financial data and a virtual gene bank; it updates financial data from public sources (Yahoo™ Finance!), does all the statistics for chosen technical indicators, and trigger training process via MetaDGPEngine.
Background
The original incentive of this project is to implement a comprehensive market analysis and prediction platform, with fast running speed, better prediction result and ease of use. To some extent, all that machines trying to do is no more than simulating a trader’s brain. And obviously differences exist. There is something machine can not do as a natural person; however, there are also advantages of machine learning: the ability of massive calculations and data storage. Hence, I start from theoretical investment analysis methodology research based on my knowledge from a previous finance degree, trying to seek a perspective suitable for machine learning. Fortunately, technical analysis, i.e., trying to evaluate those numerical indicators has always been playing a big part of a trader’s everyday job, and numerical analysis is also strength of computer.
After figuring out this intersection, we need to develop a proper solution to make use of machine’s advantages. Long ago, I have worked on an implementation of Santa Fe Institute Artificial Stock Market Model based on genetic algorithm. Other than the fact that the model is 17 years old after first proposed in 1989 (Palmer et al. 1994), it also lacks in features come from restrictions of GAs. Therefore, Genetic programming is adopted, because GP is actually evolving “strategies”, not formula coefficients. This is more reasonable for investment analysis.
Subsequently, performance issue emerged. It takes GPs on averages about several minutes for an AMD 64bit processor to find a perfect ant route (classic problem along with the first publication of GP by Koza) on a 20x20 map. Obviously for evaluation of two years historical data and technical indicators with full set of arithmetic and logical operators on stock market prediction, takes very much longer! Buying a super computer is an easy way out, but only for institutions not for profit-driven traders. Since PCs are getting much cheaper nowadays, distributed computing is considered as the best solution to encounter performance problem. Therefore, more researches had been done for this project on developing a suitable structure/topology of a distributed genetic programming.
Stock market investment analysis
Conventionally, there are two essential approaches of analyzing investments: fundamental analysis and technical analysis. In terms of stock market, fundamental analysis refers to investigating listed companies’ financial reports, related industry’s trend, general economical environment, etc. Fundamental analysis highly depends on sources and timing of information. Its accuracy can be easily biased by information asymmetry. Therefore it is usually considered as tools for long-term investment analysis.
Technical analysis focuses exclusively on the stocks’ historical data, asking what does its past behavior indicate about its likely future price behavior. Technicians, chartists or market strategists, as they are variously known, believe that there are systematic statistical dependencies in stock returns - that history tends to repeat itself. They make price predictions on the basis of published data, looking for patterns and possible correlations, and applying rules on charts to assess ‘trends’, ‘support’ and ‘resistance levels’. From these, they develop buy and sell signals. Due to its high sensitivity, technical analysis usually applied to short term prediction.
This project takes technical analysis as entry point, trying to exploit programming algorithm’s advantage on quantitative analysis. Therefore, discussion on Efficient Market Hypothesis provides the fundamental theory that proves the effectiveness of technical analysis hence the significance of this research at theoretical level.
Efficient Market Hypothesis
In a controversial paper to the Royal Statistical Society (1953), Maurice Kendall suggested that prices of stocks and commodities seem to follow a random walk, which means that successive changes in prices are independent. Therefore, no predictable cycles should persist in a series of prices. When however such a cycle would be come apparent to investors, they immediately eliminate it by their trading. Later in 1965, Fama defined the concept of Efficient Capital Market. He proposed basic assumptions to this hypothesis as:
“a market where there are large numbers of rational profit maximizers actively competing, with each trying to predict future market values of individual securities, and where important current information is almost freely available to all participants.”
In 1970, Fama further developed his theory by distinguishing three levels of market efficiency:
- The “Weak form efficiency” asserts that all past market prices and data are fully reflected in securities prices. Therefore, technical analysis does nothing to help investors make profit.
- The “Semi-strong form efficiency” asserts that all publicly available information, for example financial statements, is fully reflected in securities prices. In other words, fundamental analysis is of no use.
- The “Strong form efficiency” asserts that all information is fully reflected in securities prices. In other words, even insider information is of no use.
Base on above forms of market efficiency, if target stock market is weak form efficiency, then any research ground on technical analysis is meaningless. Therefore, we need to first study the market efficiency of target markets.
The efficient market hypothesis was introduced in the late 1960s. Prior to that, the prevailing view was that markets were inefficient. Inefficiency was commonly believed to exist e.g. in the United States and United Kingdom stock markets. However, earlier work by Kendall (1953) suggested that changes in UK stock market prices were random. Later work by Brealey and Dryden, and also by Cunningham found that there were no significant dependences in price changes suggesting that the UK stock market was weak-form efficient.
Further to this evidence that the UK stock market is weak form efficient, other studies of capital markets have pointed toward them being semi strong-form efficient. Studies by Firth (1976, 1979 and 1980) in the United Kingdom have compared the share prices existing after a takeover announcement with the bid offer. Firth found that the share prices were fully and instantaneously adjusted to their correct levels, thus concluding that the UK stock market was semi strong-form efficient.
A conclusion on the absence of weak form efficiency on stock market could greatly suggest opportunities to earn abnormal profits through technical analysis. In fact, this kind of conclusion is yet never certain. However a great proportion of the sample results from this research demonstrate a convincing ability to earn gains to certain degree. Therefore, we can at least be against the saying that technical analysis is of no use. And a better solution in search of an effective technical analysis strategy draws the purpose of this project.
Genetic Programming
Genetic Programming (Koza et al., 1992) is a recent development in the field of evolutionary programming (EP) (Fogel et al., 1966) which extends classical genetic algorithms by allowing the processing of non-liner structures. This section attempts to provide some background knowledge and mechanics of Genetic Algorithms and particularly Genetic Programming.
Genetic Algorithms in General
Genetic Algorithms (GA) (Holland, 1975; Goldberg, 1989) are stochastic search techniques working on a population of individuals or solutions encoded as linear gene belts, usually in the form of bit strings. Theoretically, GAs can be viewed as a search procedure that trying to find a solution subject to some boundary conditions. GA’s way to accomplish this is inspired by Darwin’s theory of evolution, which is based on the notion that living beings developed as a result of biological chain reactions caused by natural selection.
GAs start with an initial population of individuals or solutions to a problem. Each individual has its unique chromosome, which is a collection of genes. In traditional simple GA defined by Holland, those genetic units are mapped into binary strings. Each bit on a string corresponds to a constraint to the problem. A group of such binary strings is the population. This population evolves over time through the application of genetic operators which mimic those evolutionary processes found in nature, namely, survival of fittest, crossover and mutation. These biological operators do not work on the individuals as in nature, but on their chromosomal representation.
Parent chromosomes are selected in the population for reproduction. This process is called Selection, which is probabilistic and biased towards the best individuals. The selection procedure is vital to the successfulness of the genetic search. It propagates good solution features to the next generation. The most common form of selection method is roulette wheel selection (Goldberg 1989). The principle is that individuals are selected from the population with a probability that is in accordance with their relative fitness value as evaluated against the whole population. For example, an individual with a fitness value stands in the middle of the population. Then it has half of the probability to be selected. For GP, we use another popular form of selection method called tournament selection by Koza, as described later.
Selected individuals form a mating pool, where paired parents are randomly chosen and Crossover process is carried out. The crossover operator combines the characteristics of paired parents’ chromosomes to create two new offspring, with the aim of having better fit than their parents. A cross point is randomly chosen along the length of the chromosomes and two chromosomes swap gene information from this point onwards, thus creating two new individuals:
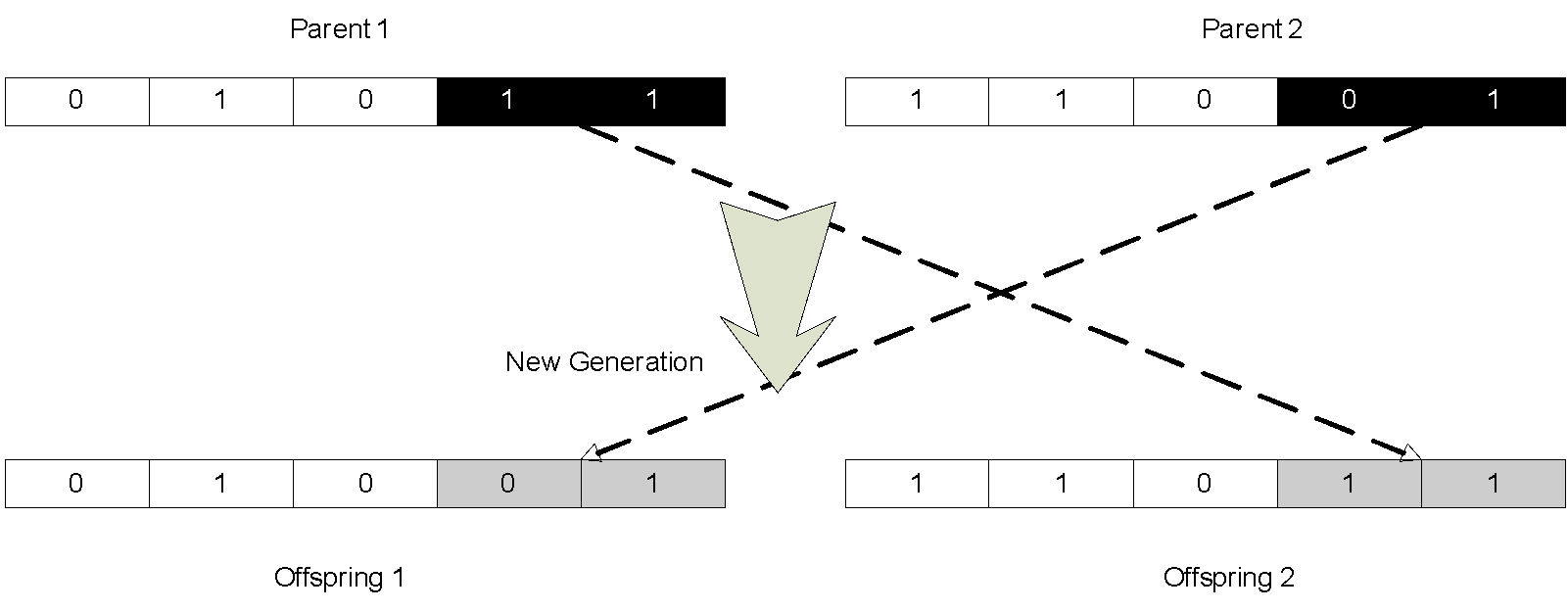
Finally, the Mutation operator is applied to a proportion of new generation, this introducing some random variation into the population. For a bit string genetic algorithm, individuals are randomly selected according to a mutation probability. A position on the chromosome is chosen and the value of the bit gene in this position is flipped from 0 to 1, or from 1 to 0. Mutation is considered only as a touch of finish that slightly perturbs small proportion of solutions.
Through the three genetic operators, i.e., selection, crossover and mutation processes, the population of individuals or solutions is expected to be continuously improved, as individuals in new generations will be gradually replaced by better gene belt. This sequential process will repeats itself for generations. Depending on the problem in question, the termination criteria can be either convergence, or a fixed maximum generation defined.
GAs have been demonstrated to be an effective problem solving tool for tackling complex optimization and machine learning problems, with a wide range of application, including imaging, circuit design, gas pipeline control and production scheduling (W.B. Langdon and Qureshi, 1995).
Mechanics of Genetic Programming
Genetic Programming extends the paradigm of bit string genetic algorithm by introducing tree structures (genotypes) of encoded programs. Therefore GP does not need to encode the problem, but generate automated programs to solve problems. This greatly expands the areas of evolutionary programming. Programs can represents anything for different problems, and GP offers a unified approach.
Most of the mechanics of genetic programming can be exactly the same as those in bit string genetic algorithms. This section describes those different ones.
Fitness Evaluation
The evolutionary process of genetic algorithms is driven by a fitness function that evaluates the performance of each individual in given problem environment. Therefore the fitness function provides a direction to the evolutionary process. It needs to be mentioned that, in genetic programming, the fitness value does not evaluate solution but the ability of finding solution for an individual in question. In this project, profit generated by individual’s investment strategy (program) is evaluated on historical financial data. More details in design chapter later.
Tree Structure Encoding
Tree structure in genetic programming consists of terminals nodes and function nodes defined for a problem. Trees are recursively constructed from this set of nodes and dynamically change during the evolution process. Each particular function in the function set takes a specified number/types of arguments and should be able to accept returned value by other functions, or terminals which do not have argument. (Koza, 1995) For example, an arithmetic expression 3 )2( × +z can be represented in tree structure as:
| Function Type | Function Examples | Inputs | Output |
|---|---|---|---|
| Logical | AND, OR, NOT, XOR | Boolean(s) | Boolean |
| Comparison | >, <, ≠, ≤, ≥ | Real numbers | Boolean |
| Mathematics | +, -, x, ÷, Pow, Log | Real numbers | Real number |
| Programming | IF-THEN-ELSE, DO-WHILE | Boolean, (delegate) | (delegate) |
The search space in genetic programming is the space of all possible computer programs composed of terminals and functions appropriate to the problem domain. In general, terminal set consists of variables and/or constants (z, 2, 3 in the above example). While function set includes arithmetic operators ( , ,,, ÷ ×−+ etc.), mathematical functions (Sin, Cos, Log, etc.), logical functions (AND, OR, NOT, etc.), and programming functions (IF-THEN-ELSE, etc.). Genetic programming possesses the elasticity that bit string genetic algorithms lack, therefore it can search even wide and complete problem space.
Initial Population and Tree Creation
Similar to other genetic algorithms, initial population in genetic programming is made of randomly generated chromosomes, but in the form of programs trees. A good tree creation algorithm is important to GP. It is because that, initial population creation plus new branches of tree in crossover and mutation procedure could result at least 100,000 tree creations for a 100 population size in several generations. By far, the most common mechanism for creating trees and sub-trees in GP is the GROW and FULL methods. They are used in almost all literatures on GP.
GROW begins with a set of functions to place as nodes in the tree. It recursively call itself, by selecting a root from the set of functions, then fills the root’s arguments with random functions, then their arguments with other random functions or terminals, and so on (Luke, 2000). A pseudo-code can be written as:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Given:
Maximum depth D
Function set F consisting of non-terminal set N and terminal set T
Do:
New tree T = GROW(0)
GROW(depth d)
Returns: a tree of depth <= D-d
IF d=D, return a random terminal from T
ELSE
Choose a random function f from F
IF f is a terminal, return f
ELSE
FOR each argument a of f
Fill a with GROW(d+1)
Return f with filled arguments
GROW method is also extensively used in generate new sub-trees at a chosen point. FULL is merely at opposite direction of GROW procedure (not from root but from terminal nodes backwards). However, GROW tree-creation algorithm has serious weakness. It offers no control over newly generated tree, in particular the tree size. Also, for this project, GROW method can not offer fine-grained control over expected probability for a particular function/technical indicator. A better algorithm for tree creation (PTC) adopted in this project will be described in design chapter.
Genetic Programming Crossover Operator
Crossover in genetic programming is far more complicated than in bit-string genetic algorithms. The complexity comes from tree manipulations. When a crossover procedure applies on two chosen parents, a random crossover point is chosen from each parent. The crossover point defines a entire sub-tree lying below the crossover point. Two new generation programs are then produced by exchanging the two sub-trees. This better is illustrated to make clear as below:
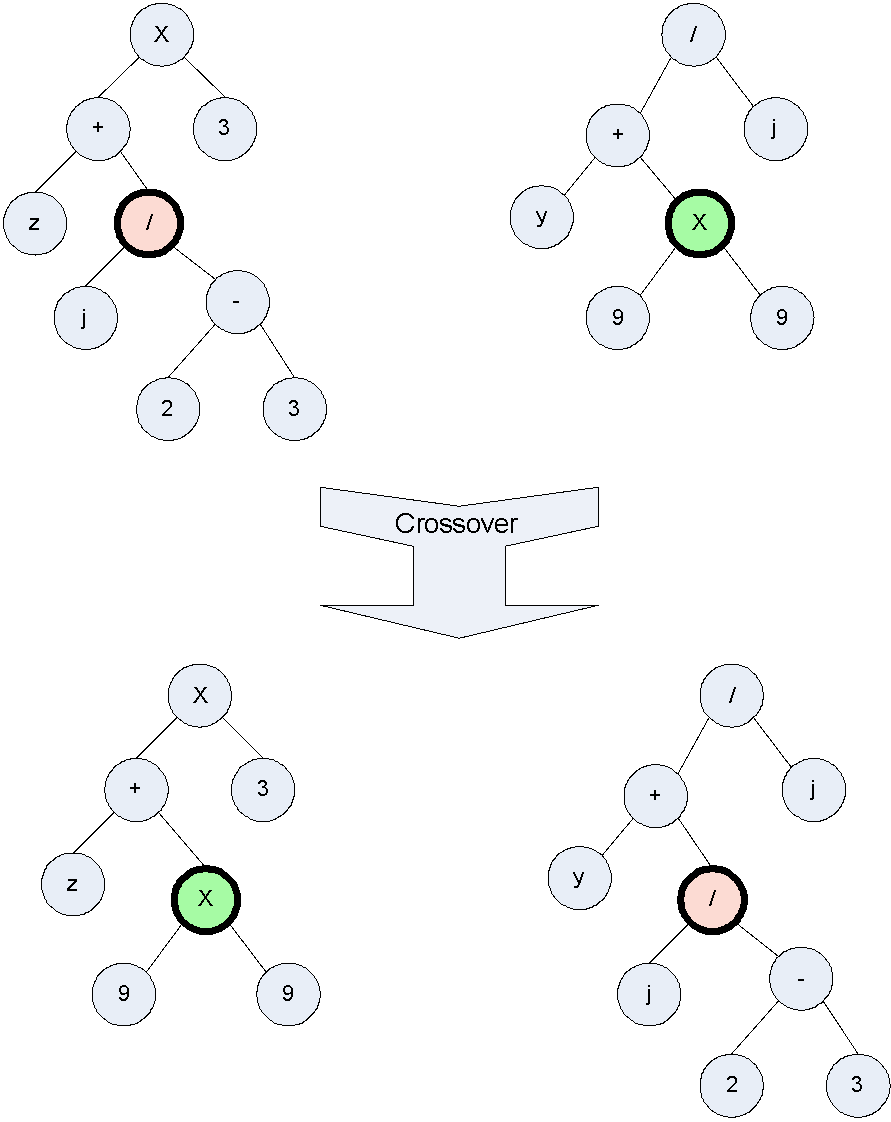
When both crossover points are terminals, only ‘leaf’ of the tree is swapped. Therefore, the probability distribution for the selection of a crossover point favours the exchange of subtrees rather than terminals. Also in this project, different financial indicators would return different type of values (floats, percentages), and different functions would have different types on return value and arguments, for example, “+” operator returns a real number and requires two arguments of numbers, while “>=” returns a Boolean value and requires two real numbers. Therefore crossover point can not be purely randomly chosen for stock market prediction problem (and most other problems as well). The crossover procedure in genetic programming need to consider a lot to guarantee compliable and executable programs generated. This will be implemented by runtime reflection, more details in Design and Implementation chapter.
Genetic Programming Mutation Operator
Mutation is still a unary operator that alters part of a chromosome, aimed at restoring diversity in a population by applying random modifications to individual structures:
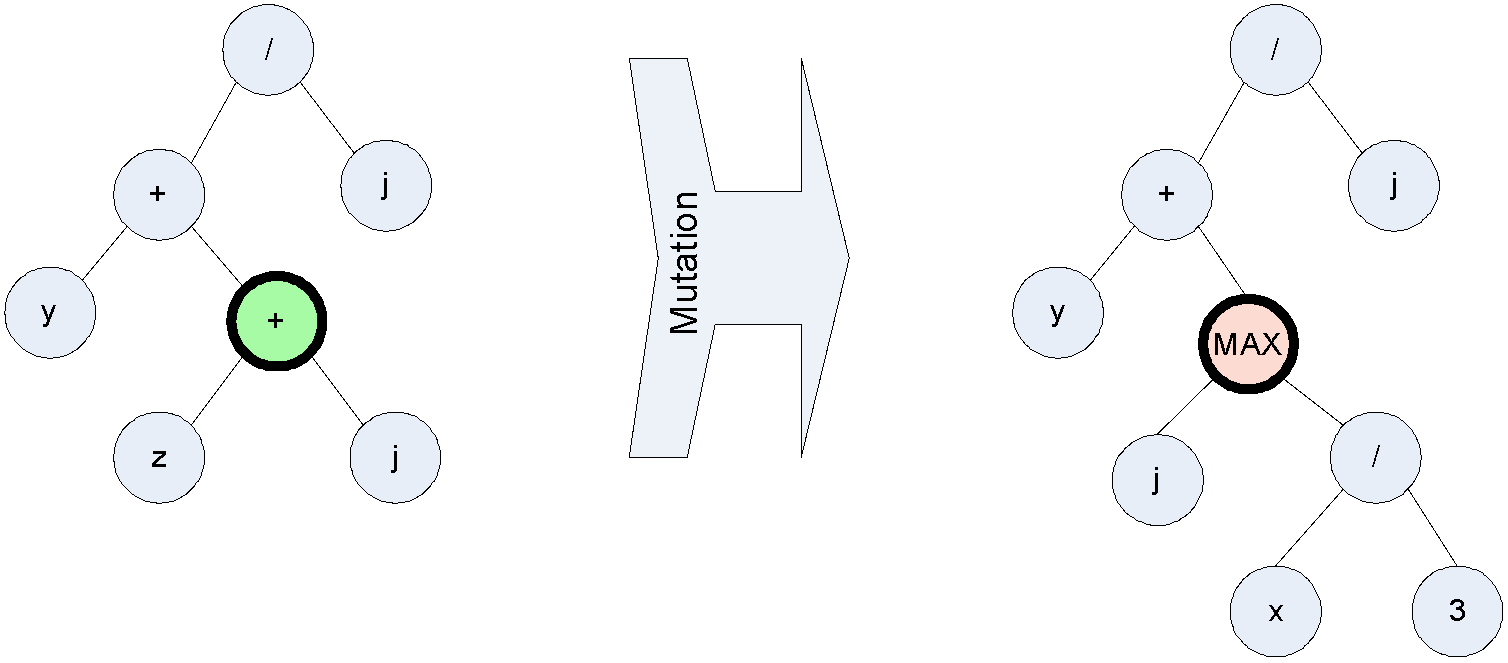
However, in genetic programming it has reduced functionality compared to its importance in bit-string genetic algorithms. Because trees manipulated in GP are far more complicated than the linear structures of GAs. Even crossover operation applied on two identical chromosomes would give completely diversified new trees. In essence, this is due to the fact that genetic programming is evolving programs not solutions. Hence it does not need mutation to maintain diversity as important as in linear genetic algorithms for coefficients. Therefore, mutation rate is kept low by default, but still exists in my implementation. It is simply done by drop a random sub tree then grow a new sub tree from that point.
To sum up, typical evolutionary steps for genetic programming are:
- Randomly create the initial population
- Repeat:
- Evaluate the fitness of each individual by execute its program.
- Select parents from population using selection strategies
- Generate new population using genetic operators: Reproduction, Crossover, Mutation
- Until termination criteria, usually a fixed number of generations.
Distributed Genetic Programming Parallelisms
This section provides theoretical research on parallel genetic programming algorithms. The reason and motivation for parallelism is firstly assessed. Followed by a survey of current literatures on schemes/topologies defines a parallel genetic algorithm’s structure. This section looks at fundamental building blocks, more details on parallel pattern of this project can be found in design chapter.
Motivation
The probability of success in applying genetic algorithm to a particular problem often depends on the adequacy of the size of the population in relation to the difficulty of the problem. (Harik and Miller, 1997). Since the computational burden of GAs is in accordance with size of population, more computing power is required to solve more substantial problems. Increases in computing power can be realized by either increasing the speed of a single computer or by parallelising the application. This is because those fast serial super computers are expensive and rare. Therefore, parallel implementations could be a more favourable solution.
Firstly, a parallel genetic algorithm does not lose any advantage of a linear/serial genetic algorithm. If we see the distributed network combined as a whole, or more specifically, a multiple-instruction-multiple-data (MIMD) (Flynn, 1972) computer as described later in feasibility assessment, there is no difference to the process from start to the end. However, a parallel distributed GA can search from multiple points in the search space simultaneously. This offers a wider search space than a serial GA. Further, since physically each paralleled GA subgroup operates on separate processors, the search speed and computation power adds up together. This offers a deeper precision on a given generation. Altogether, it is easy to see that parallel GAs have higher efficiency and efficacy than serial GAs.
Feasibility
In a previous section, we see genetic algorithms are basicly trying to mimic natural evolution. If we are adopting this process as much as in reality, then the whole process should not operate only on a single population. In nature, species tend to reproduce within subgroups or within a given circle of neighbours. An individual should have the potential to mate with partner in the entire population (panmixia or meta-population). This is where my MetaDGPEngine’s ‘Meta’ 15 comes from: meta-population. An important component of speciation theory in Biology is the deme concept (Mary, 1963) because this is the unit on which either selection or drift operates. Demes are random mating sub populations. A classic diagram found in almost any biology textbook on population structure looks like below:
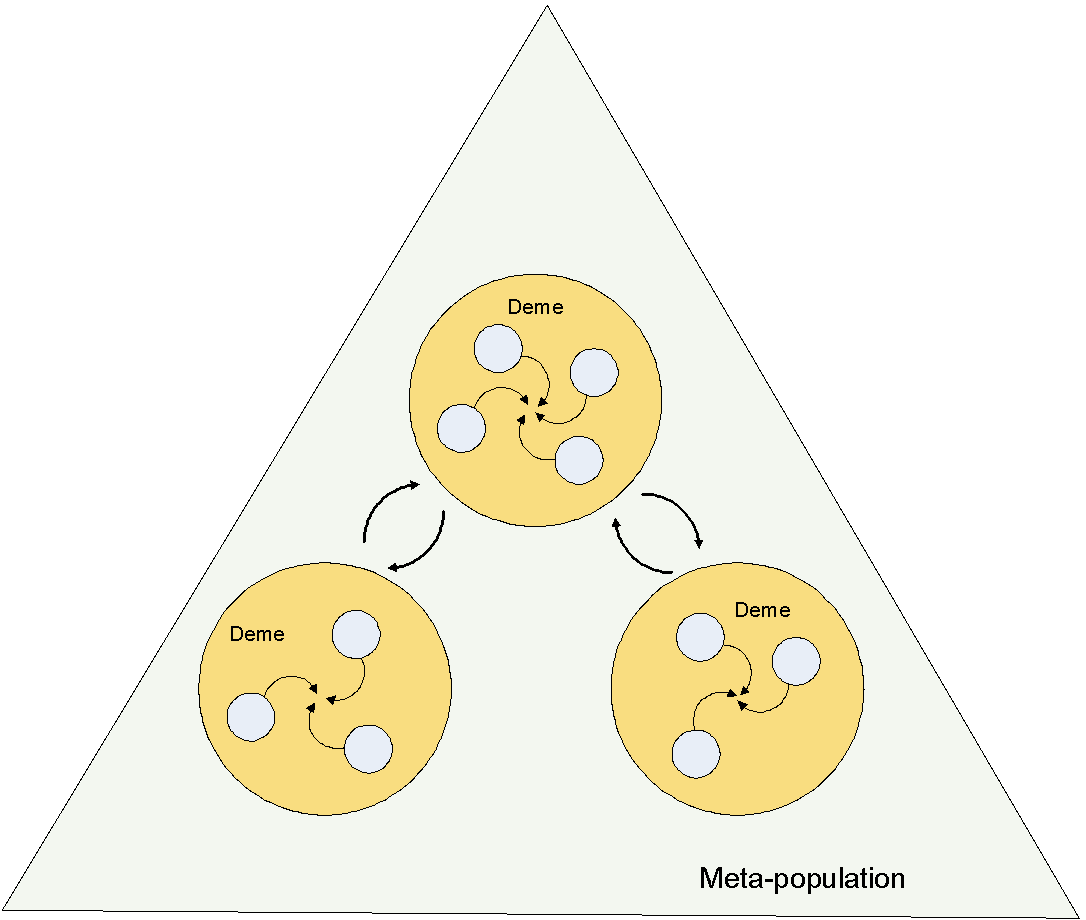
Now a distributed genetic algorithm is theoretically backed by its fundamental theory adopted from biology. But is a computerized implementation possible?
Based on Flynn’s classification of computer architecture (Flynn, 1972), a multiple-instruction-multiple-data (MIMD) are processors may perform different instructions on different data. MIMD is the most common type of parallel computers. A MIMD multi-computer is where communication between processing elements is via message passing, as opposed to shared memory in a multiprocessor machine. The approach of multiple computers connected in a P2P model for mass computation conforms to this definition, so are all of the schemes on genetic algorithm parallelisms described in following sections.
In terms of cost, for a similar level of computation power, multiple cheap desktop processors operating as grid computing is far less expensive than a single super computer. One might argue about the communication speed, since distributed programs use network connections to transfer data, whilst super computers use high speed dedicated BUS. However, for genetic algorithm problems, once well designed, this transaction cost is very much low, because most of the time genetic algorithms are doing evaluations which involves no communication in between individuals (collusion among artificial traders is an exception not belongs to the topic of genetic algorithm).
Task Allocation Modelling
There are many ways to divide tasks of the genetic algorithm process and prepare for parallelising. Firstly, let us look at an abstract model of a traditional serial GA process:
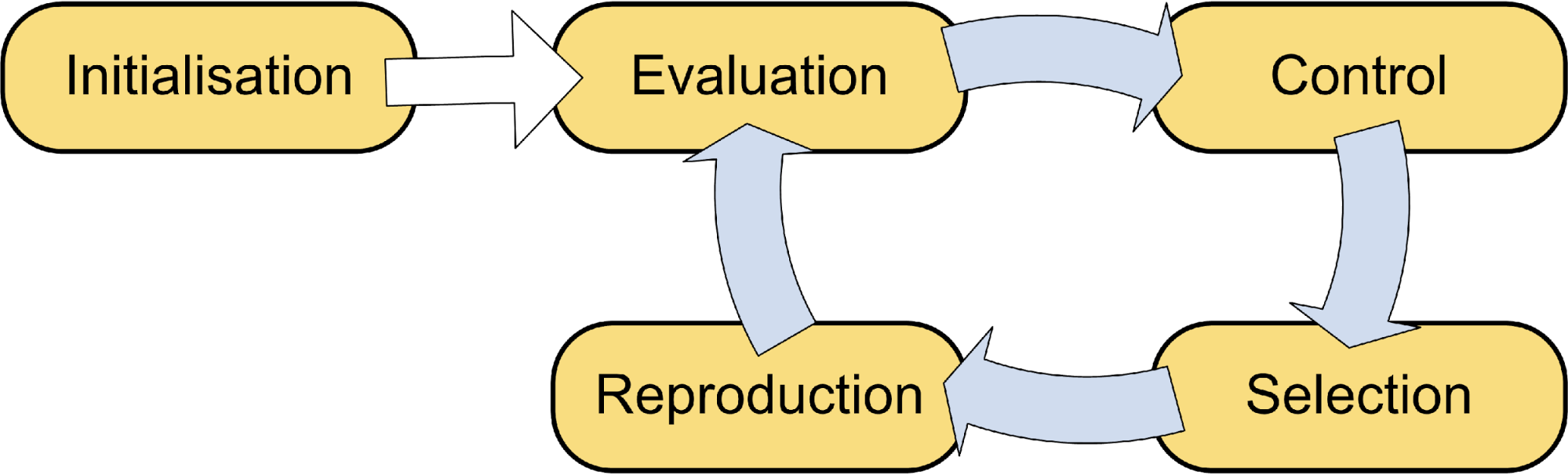
Statistically, most time consuming calculations lies in the evaluation part, and for genetic programming, the genetic operators on tree structures. Therefore, a client/server sub-task model is illustrated as follow:
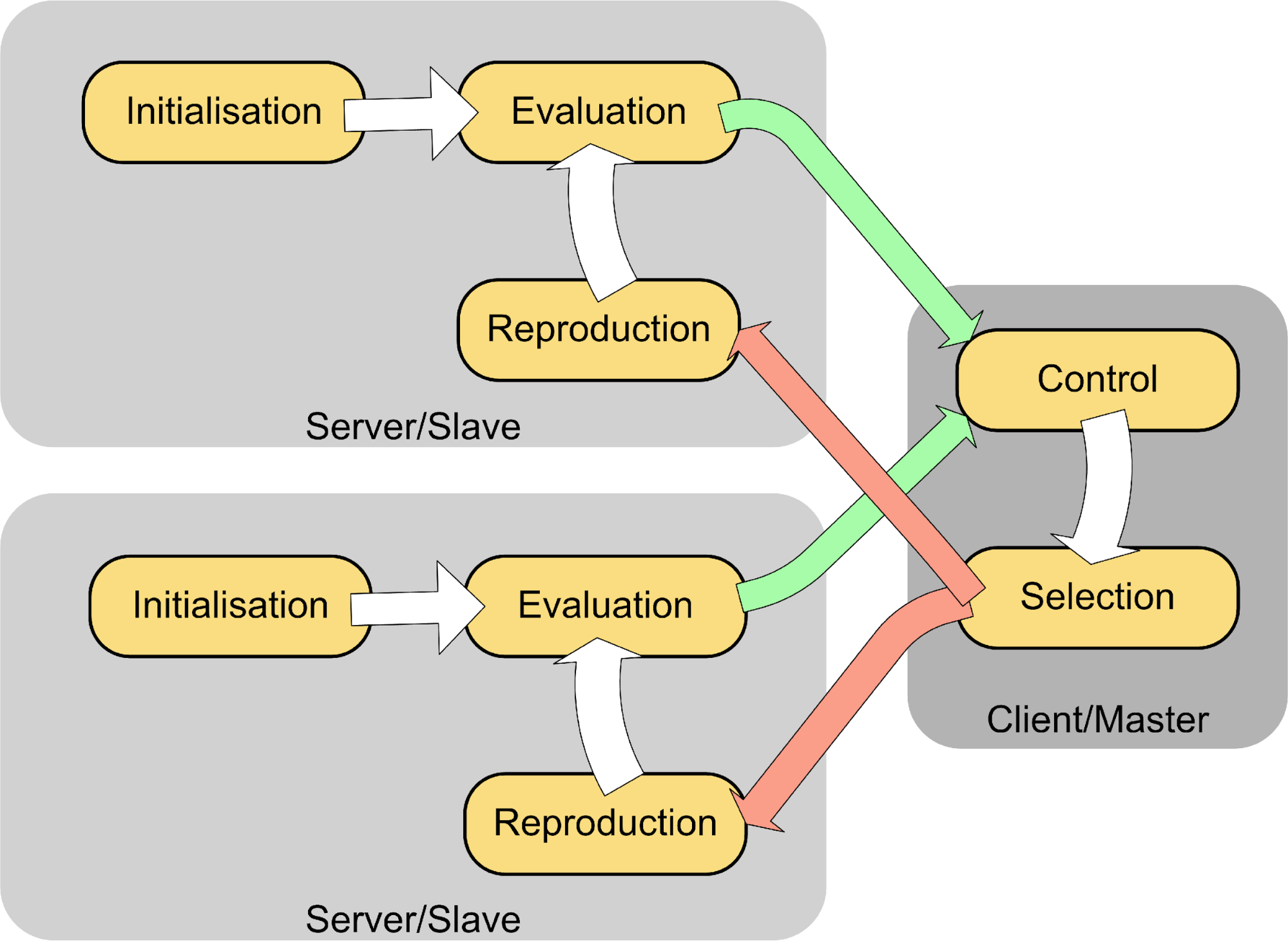
The client/server model expands server’s ability by shifting majority parts of process to multiple clients. Further to this model, recent years see the great emergence of peer-to-peer network applications. In term of genetic algorithm, it also means all process is computerised on separate processors/nodes; good individuals are exchanged in between. This is more applicable for this project, since financial prediction requires extensive calculations on almost all four sub-procedures. The above client/server subdivision model is not very much effective on stock market predictions distributed genetic programming. In a peer-to-peer model, Multiple Genetic Engines may be interlinked using a peer-to-peer network to form large virtual populations. (Individuals are exchanged during Selection phase):
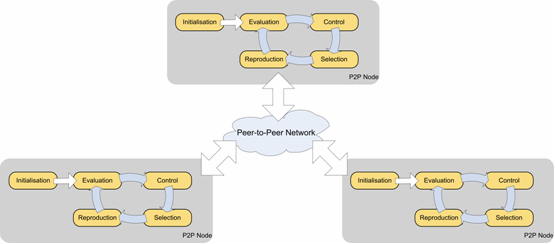
In this project, a pure P2P task allocation model is chosen for both efficiency and simplicity. However, assessing task allocation models is only part of the whole genetic programming parallelism in this project’s background research. We still need to define a topology for distributed network targeted at genetic algorithms. There are already numberous literatures on 18 this topic. And Dr. Enrique Alba and Dr. Jose M. Troya did a nice survey of parallel distributed genetic algorithms direct to this topic (Alba and Troya, 1999). Therefore the next section we simply make a summery of the advantages and disadvantages for each.
The Schema Theorem
This is the final section of background research for this project. Yet we have examined the mechanism behind genetic programming; we also have studied varies models to support a parallel distributed genetic programming system. Now we need to prove in theory that a distributed genetic programming does work. In a survey of parallel distributed genetic algorithms conducted by Alba and Troya, they adopted a Schema Theorem well supports all the rationale we have described above (Alba and Troya, 1999). Hence provides the rest theoretical foundation on the significance of this project.
Alba and Troya introduced a terminology called schemata, which acts like sub elements that logically break down a chromosome of an individual. The search space of any genetic algorithm is nothing but large quantity of good and bad schemata. And an ideal solution is simply a combination of good schemata on all parts of chromosome. Below is my illustration of understanding on this idea. For simplicity I only drew bit-string chromosomes, but this also applies to tree structures in genetic programming.
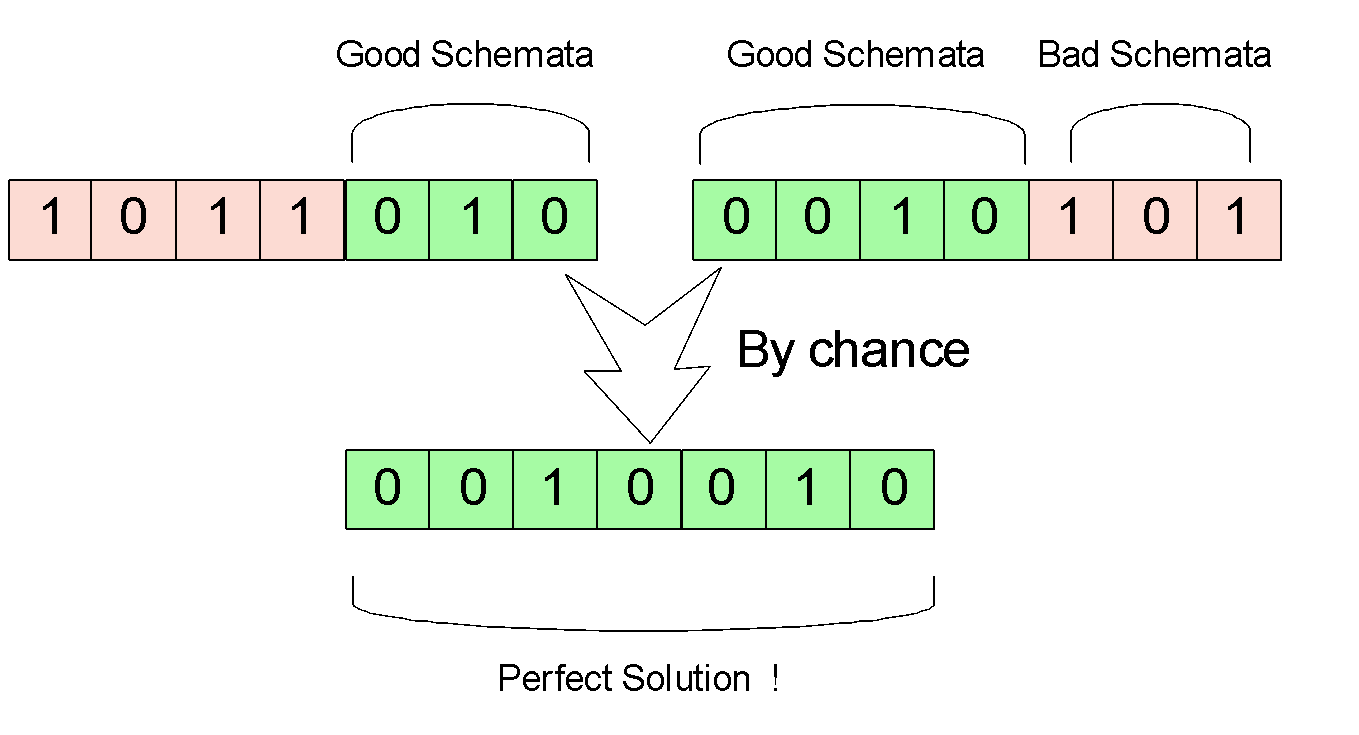
In an initial study by Holland, he worked out a result known as the implicit parallelism of evolutionary algorithms. He suggests that although the genetic algorithms are working on chromosomes, the whole mechanism is actually working in a 3-Dimensional space of schemata. (Holland, 1975). Alba and Troya extend this theory. By trying to modelling the effects of genetic operators, they conclude that crossover and mutation process are actually filtering good schemata. Therefore, any problem that can be expressed as building blocks can be solved by genetic algorithms. For example, bit represents co-efficiency on bit-string; tree node represents a function or variable on a genotype as in genetic programming.
Furthermore, Alba and Troya extend their Schemata Theorem trying to prove distributed genetic algorithms. This was developed upon an existing measurement of merit of parallel genetic algorithms developed by Goldberg (Goldberg, 1989). Under the assumption that each individual perfectly acquires a separate and identical processor, the merit of a parallel genetic algorithm depends on the population size, string length, and degree of parallelism. Below I used their graph to illustrate this relationship (Alba and Troya, 1999):
By applying the relationship between degree of parallelism and number of strings in given population, they finally conclude that the assumption is not necessary. That is to say:
a high performance distributed genetic algorithm does not depend on an ideally perfect parallel hardware. (Alba and Troya, 1999).
Having every element of the rationale behind the whole project theoretically proved or supported, we now can lead to see the design issues.
Design
The aim of this project is to implement a visualised distributed genetic programming system applied on stock market prediction. Therefore, from a direct literal interpretation of this title, we need to design a parallel distributed genetic programming system; then a mod on financial genetic programming; finally it needs to be visualised. There are numerous literatures working good or fine on each of the sub element, however, until I am writing up this report, there is no such a comprehensive visualised system that creates and combines all these parts. In this chapter I shall talk about various important design issues involved in building up this system.
Island Model Distributed Genetic Programming
In a previous section, we have assessed many design patterns on parallel distributed genetic programming system architecture. And by comparing advantages and disadvantages, we have chosen a coarse grain parallel genetic programming model as the best candidate for our project, since it mimic the nature’s population structure at the best, also very much suitable for our chosen P2P network task allocation model. However, a theoretical pattern is far from a working system’s implementation. There are still lots to think about. Especially, the inter-communication between each demes within our meta-population.
Deriving the Controlled Coarse Grain Parallel Genetic Programming Model
As an overseas student, I travel in between continents a lot each year. This summer I took this project’s initial specification with full of question marks back home. When standing in the long queue at the very familiar passport control counter, it suddenly inspired me a working model for this distributed system. Those individuals travel in between demes (or countries, as I called it initially) can be viewed as migrants. Later after I rushed into library referencing how population structure defined in biology, I found exactly similar set of terminologies as expected. There is a mainland-island model of biological eco-system defined. And individuals migrate between islands and mainland. I illustrate it as below:
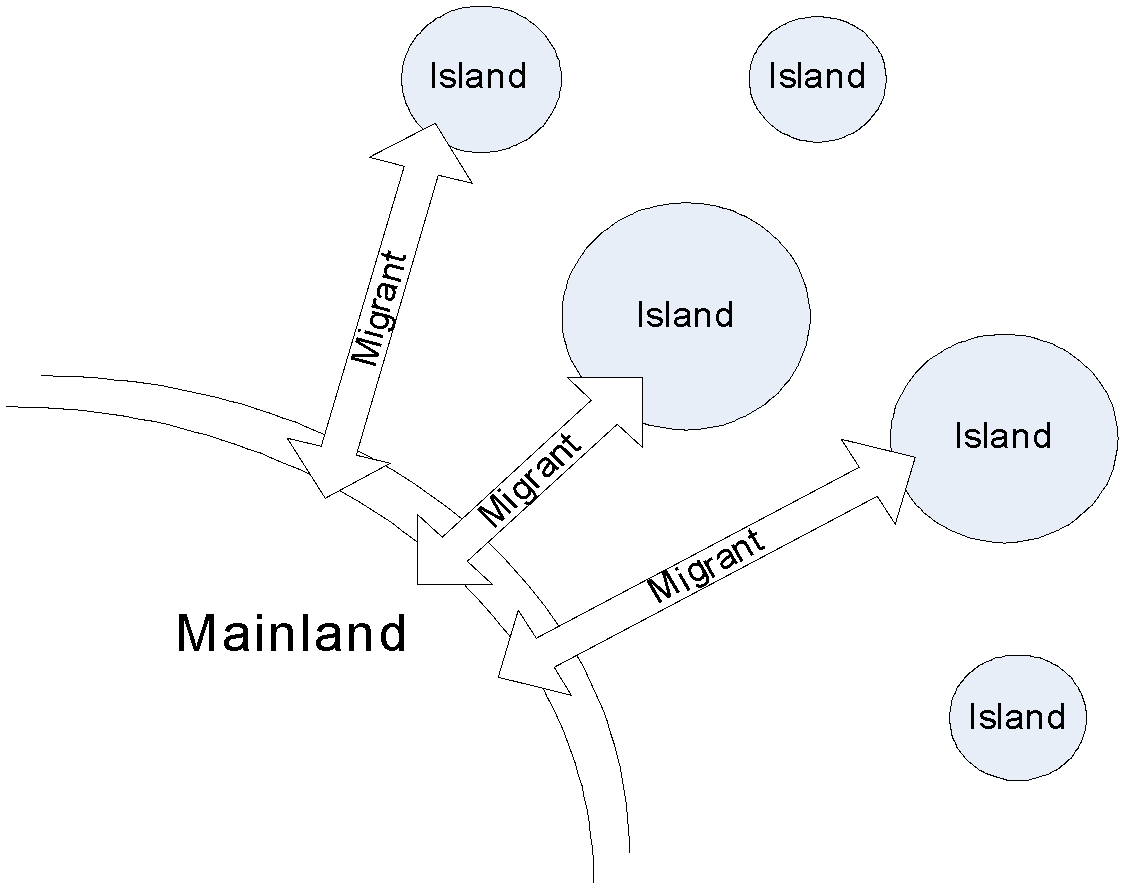
Therefore, instead of a collection of discrete peer nodes, which is ideal theoretically but lack of control in application. I modified the coarse grain parallel model into a somewhat controlled model:
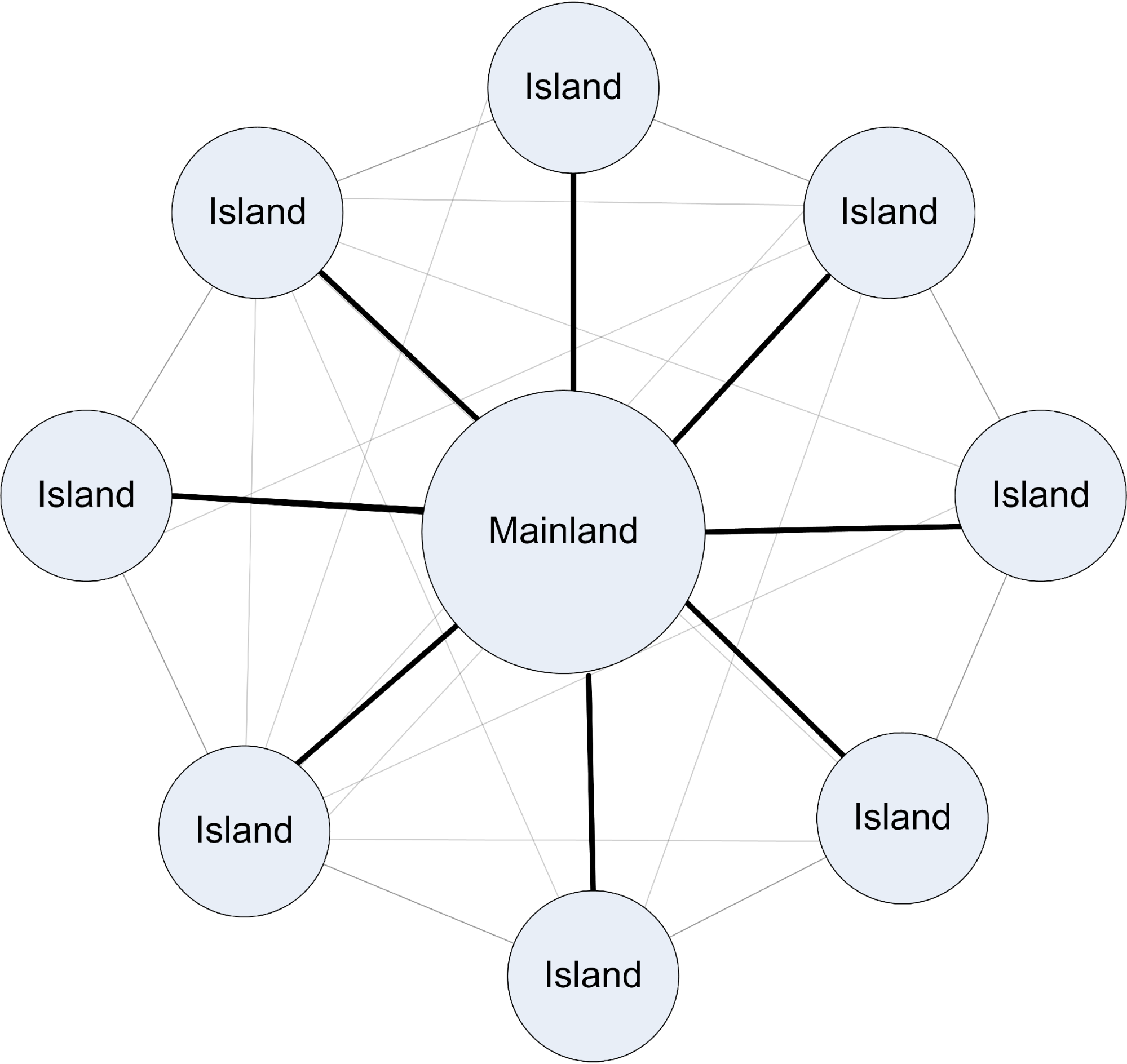
As in the graph above, individuals travel in between islands and mainland, only through thick lines. Those transparent lines only illustrate the abstract process of good migrants travel among islands, which is actually controlled and selected by mainland. This is how only good migrants are delivered (broadcasted) into other islands. Therefore mainland can control the whole population. In my system, the mainland does not take on genetic procedures; it merely does the control part. Firstly, this avoids the traffic problem in global parallelism. Controlling server can use this released computing power to achieve other task, for example those flashing animated visualisation without any delay in this project. Second, the existence of a centralised management makes the whole system easy to use and more reliable. Any failure island would not affect the whole distributed system. Each island can connect and join into this distributed network anytime but start with breeding new generation from the latest migrants. Moreover, we can use linear method to test the performance of the distributed system, for example, statistics on the performance of each processing node is collected in this project.
It is when I am writing up this report, that I found out the notion of “island model” has already been adopted on parallel genetic algorithms recent years in different ways. This further proves the feasibility of such a distributed system structure. Tanimura adopted this model to develop his Dual Individual Distributed Genetic Algorithm (Tanimura, 2000). Whitley, Rana and Heckendorn studied how to use linearly functions to test an island model distributed system (Whitley et al., 1997). Vertannen discussed the island model under parallel virtual machine (PVM).
Migrants Pool
A finished model for island and mainland is still not enough for implementation. How does mainland manage migrants? How is migrants selected to broadcast to other islands? In this project, a migrants pool is designed to meet this requirement. Mainland maintenance a migrants pool which is in essence a collection of queues for connected islands. Given that island only sends out new better individual in each generation, this queue is designed to be LIFO for all other islands, so that the best is always floating to the top.
For every beginning of a new generation in each island, the best individual from last generation is sent as emigrants to mainland. Then it tries to collect all new individuals as immigrants from others’ migrant pool stored at mainland. These new immigrants will be combined into island’s mating pool to produce the next generation. Below is an illustrated graph for this process, this is also the prototype for visualisation in the actual application. The animations implemented in project application make this process clearer.
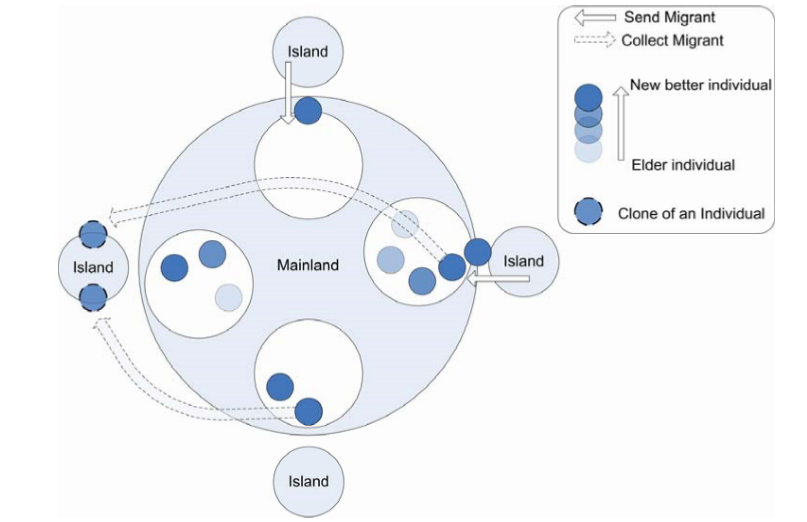
Once an individual become a migrant, a GUID is assigned, which is unique in all meta-population, and even for any runs of genetic programming meta-populations. This is designed to make sure individuals can be recognised, also for storage in a Gene Bank database which will be described later. A migration history is attached to each individual in migrant pool to avoid duplicated migration, i.e., clones any individual only need to migrate to mainland or any island once.
Genetic Programming
The procedure of genetic programming under our model is conducted in each island. In fact each island is a P2P node in a previously assessed model for task allocation. Island responsible for all processes involved: initialising population, evaluation, reproduction, crossover, and mutation. The parameters are collected from mainland server when island trying to connect. Basic parameters for genetic programming algorithm and default values are listed below:
| Parameter Name | Default Value |
|---|---|
| Population Size | 200 |
| Terminating Generation | unlimited |
| Reproduction Rate | 35% |
| Crossover Rate | 60% |
| Mutation Rate | 5% |
| Max Tree Depth | 17 |
| Max New Sub Tree Depth | 6 |
Financial Genetic Programming
One of the goals of this project is to achieve a precise and efficient stock market prediction, through distributed genetic programming. There are many research papers working on bit-string genetic algorithms, but less on genetic programming. In background chapter, we already proved in theory that genetic programming is more suitable for financial prediction. But the mechanism of design and implementation remains a blurred area.
In this project, the return is investment gross profit. Because trader can profit from both positive and negative price moves. If the price is expected to go up, then a trader would take long position, i.e. buying stock and selling later; if the price is expected to go down, then a trader sells to take a short position then later buys. A higher percentage return is possible if one takes long and short position on margin. And in margin trading, traders only need to pay half of the commission.
Therefore, for genetic programming, we are generating investment strategies based on returns rather than price valuation formula. This also has the advantages that transaction costs can be taken into consideration, which has to be ignored in bit-string genetic algorithms. A typical parameter setting for short-term financial genetic programming defined in this project looks like:
| Parameter Name | Default Value | |
|---|---|---|
| Investment Cycle | 14 days | Short-term (2 weeks) investment cycle |
| Required Rate of Return | 4% | By default, the lowest return should equal to interest rate |
| Transaction Cost | 5% | This sets a constraint that requires strategy generated to be rational on trading frequency |
In summary, we expect our strategy programs to generate signals rather than price predictions, which is closer to traders’ decision considerations. Signals are same to that credit rating commonly on all financial reports. In this project, BUY, HOLD and SELL are signals adopted.
Strategy Programs
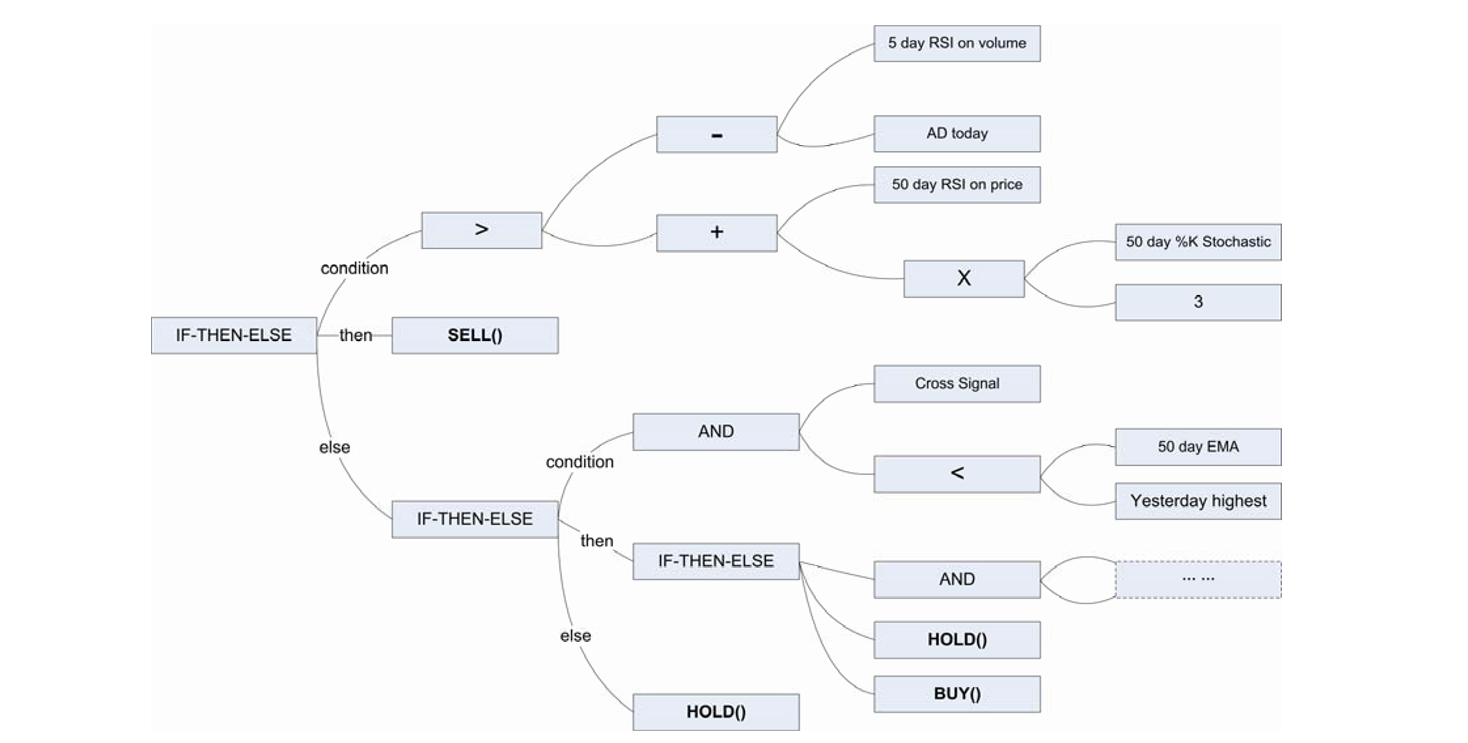
We expect genetic programming to generate investment strategies for financial market prediction. How are those strategy programs defined? Just like technical traders, the strategy programs should use technical indicators as input, and by trying to find the relationships, eventually derive a program that could generate signals. An example from the result of this project, e.g., a profit making strategy programs on two years historical data for Microsoft (MSFT) obtained after 87 generations is:

Internally this program is in tree structure representation, this is illustrated as below:
Selected Technical Indicators
The first question is why we need technical indicators, since all technical indicators are nothing more than some mathematics tools applied on raw data. The raw data for any financial market assets are merely Open, Close, High, Low, Volume. Our genetic programming already contains arithmetic and mathematics operators which could also obtain similar result as any indicator. Besides the fact that calculated indicators could greatly speed up our genetic algorithm process, indicators as investment measures commonly adopted by traders can also help our programs to be human-readable.
There is no literature yet on selecting appropriate technical indicators for machine learning. Either some are trying to include all, or some merely use moving averages on price. I did extra research into this area. There are large quantity of indicators available, some are popular, some are characteristic. In general, these indicators fall into categories, from both mathematical and data type perspectives. Therefore a sound way is to cover these area one by each: We do not need to include every indicator, but we need to keep the balance and efficiency of indicator set. In addition, most research have been focusing on price indicators, but ignore volume, in reality volume takes a very much important role on measuring psychological effects in stock market. Hence it also forms a big category in this project. Below is the table of indicators adopted, listed in a form crossed by characteristics and data types:
| On Price | On Price and Volume | On Volume | |
|---|---|---|---|
| Moving Averages | Median Moving Average | ||
| Stochastic | %K Stochastic | ||
| Momentums | Momentum Percentage | ||
| Oscillators | Relative Strength Index (RSI) on price | ||
| Accumulative Distribution | Chaikin Money Flow |
Explanations on each indicator are beyond the scope of this report. More details can be found in Appendix.
It needs to be mentioned that most indicators have length of period as a parameter. For example, there are 5 days, 10 days, and 50 days MovingAverage. This is represented in strategy programs as EMA5, EMA10, EMA50. Also, most of time the program need to compare with historical data or indicators, this is represented in strategy program as HIGH[n-2], which stands for highest day price two days ago.
Based on the flexible genetic programming engine implemented in this project, it is also interesting to mention that there is one extra indicator that returns a boolean value, as seen in the strategy program example in last page: CSP(). This indicator returns true when a long period indicator is crossing a shorter period indicator. This was a favourite short-term indicator mentioned by my mother, a long-term market speculator. When this is added to function set of this project’s financial genetic programming system, it is interesting to observe that for a number of generations at the beginning, all islands stuck at this “best” indicator, since no other combination can beat the profit generated by this simple strategy:
IF CSP()
THEN BUY()
ELSE SELL()The above tree output is always the first migrated individual for almost any setting. This demonstrates this project’s ability of searching solution. However, this strategy is then quickly replaced by better strategy programs consist of complex grammar. This proves the working evolutionary algorithm of this project.
Hypothesis Investment Strategy for Evaluation
Having decided the structure of our strategy programs, we need a scheme to evaluate the performance. And we need it to return a fair fitness value for genetic programming procedure. Initially, works has been done trying to develop a percentage precision on prediction. But how do we measure the accuracy of a strategy program? Again I realised that this is for price prediction. We need to have different tool for return/profit measurement. It is also required to be comparable for different assets/stocks.
A hypothesis investment strategy based on investment cycle is defined for evaluation of financial genetic programming. Initially every individual has a zero holding (fitness value equals 0). Whenever there is a BUY or SELL signal placed at a particular day of historical data, we buy or short sell one unit of currency (e.g. 1 sterling) at that stocks current price. Within the period of investment cycle, for example 14 days from the trade is made, if return rate (profit margin) at any day beyond the required return rate (4% by default), then we sell or buy back this asset. If at the end of investment cycle from the day trade was made, the return rate on any day below the required return, we force to sell or buy back this asset. This is implemented by attaching an account book for each individual during evaluation procedure.
This hypothesis investment strategy for evaluation test implements following features:
1. It is based on profit returns.
2. By standardising one currency unit per trade, it provides a comparable fitness value for different individuals in one population and populations for different settings of test.
3. It put investment cycle and required rate of return into practice, and give them meanings in financial genetic programming.
4. Fitness value is not capped as it should not be in financial prediction: there does not exist any set of 100% accurate trading activities in any context.
Visualisation
Visualisation adds value to distribute genetic programming. Firstly, visualisation assists performance study of genetic programming. Adjustments doesn’t need to be made after waiting for a long time to gather data and put them into statistical package finally get the same set of graphs. A real time rendering engine provides an efficient and effective tool.
Secondly, a distributed network need a system to control and manage, there is nothing else better than a visualised platform. Especially for financial users, they do not want to or do not have enough time to understand academic models behind distributed genetic programming. A visualised animation explains everything straightforward.
The visualisation of this project needs to implement following features:
1. Each elements need to be represented: Island, Individual migrants, Current best individuals.
2. A rolling message pane is needed to inform user what is going on in real time.
3. Statistical graphics need to be presented and updated in real time.
For a common design in graphcis area, we need a script system and a fast graphic rendering engine to accomplish these, which are exactly the same as technologies used in game development. My MetaGraphicEngine implemented all above and beyond, it can be easier expanded. Also interfaces are defined internally in between MetaDGPEngine and this graphical engine. It is very much easy to add more information or statistical graph to our visualised interface. The graphical engine needs to run in separate thread so that it does not affect the performance of MetaDGPEngine.
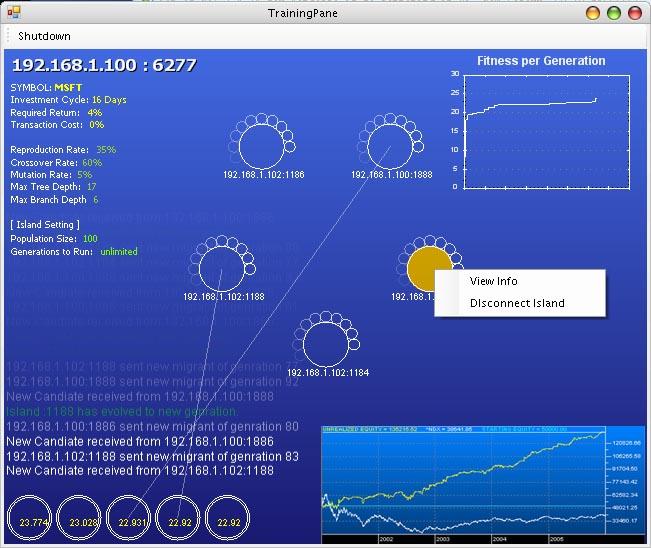
Below is a typical screenshot of the running application’s training pane, screenshots can not demonstrate transparent vector animations implemented by my 2D graphic rendering engine.
Application Structure
A comprehensive application structure needs to be designed to support such a rich content software package. At the beginning of development of this project, I have decided that a generic distributed genetic programming (DGP) engine needs to be implemented first and bug free. Then a graphical engine and modules for financial genetic programming are added thereafter. This provides good milestones to schedule the development of this project. In terms of final product, we also have a generic DGP engine and a 2D vector graphic engine reusable for future projects.
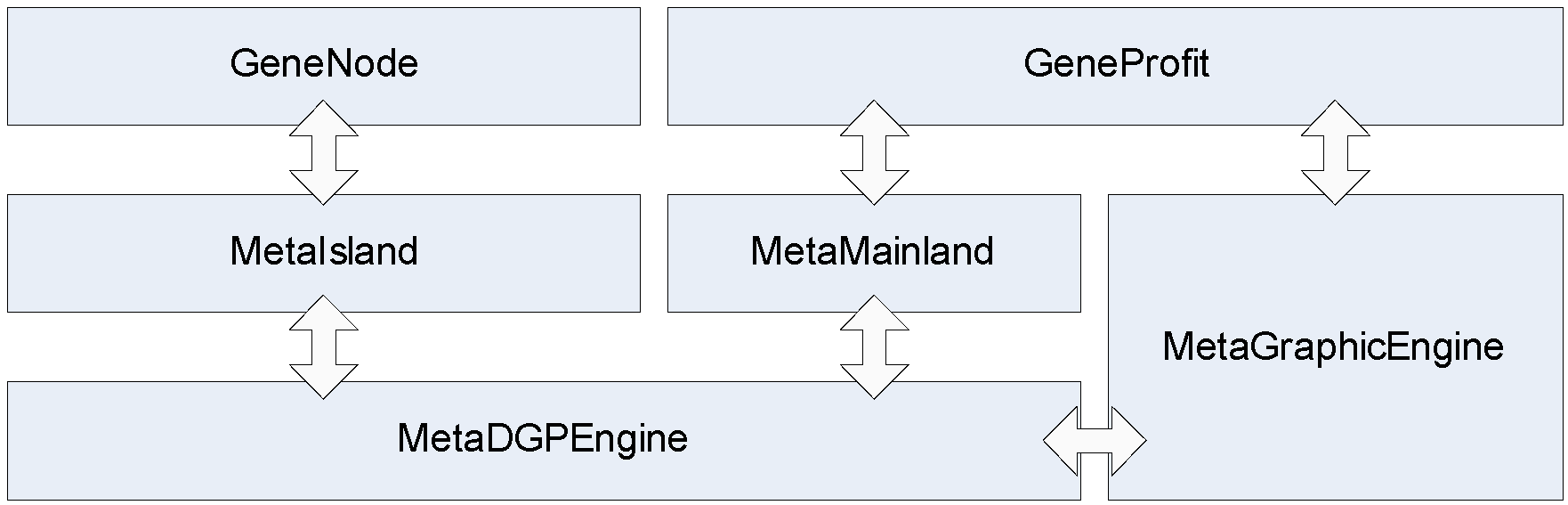
Meta Distributed Genetic Programming Engine (MetaDGPEngine)
MetaDGPEngine is a generic DGP engine that implements all related models described yet. Here theoretical models are finally coded.
In terms of genetic programming, MetaDGPEngine’s tree genotype accepts all user defined types, and has internal syntax check to guarantee generated programs can be compiled.
Controlled coarse grained parallel distributed network is implemented by TCP socket. The reason is that I design this software package to be used in intranet, rather than P2P over internet. Although migrants fit more into UDP packet, a continuous connection between islands and mainland is favourable for control and management. More detail in implementation chapter.
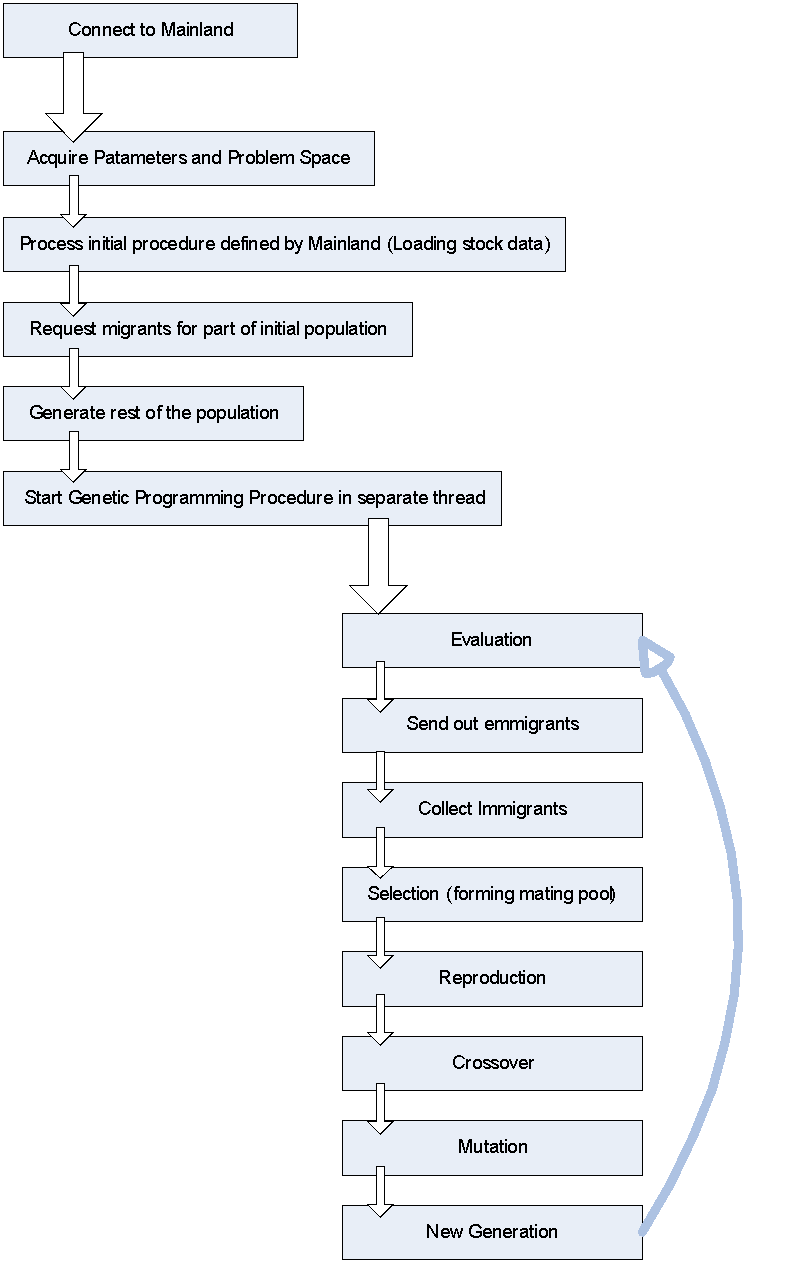
MetaIsland
MetaIsland is the implementation of islands in Island Model. Ideally it does not need to worry about the problem space, this information should be provided by mainland once connected. In my implementation, the MetaIsland requires completely zero configuration. (Except server address since we do not want to enable host discovery) Its only job is to repeat genetic programming procedure. The basic control flow of MetaIsland is illustrated as:
MetaMainland
MetaMainland is essentially a TCP server. Once started, it listens to server port for incoming messages and process messages. Features of the TCPSocketServer implemented in this project are described in implementation chapter. The server needs to have a good load balance, scalability, and vulnerability. MetaMainland has a basic authentication to ensure connections are from MetaIsland clients. Incoming messages are mixed by commands and datagram. I have designed a command system similar to FTP for intercommunication between island and mainland. Datagram may contain parameters, binary programs, and serialised individuals.
Meta Graphics Engine
MetaGraphicEngine is a 2D vector graphic engine. With the aim of encapsulation and ease of use, it has a similar script commands as in game development, to automatically generate animations in between any two key frame. As a freelance designer, I borrowed this idea from my familiar designing package Macromedia Flash™. Each action of an element takes arguments of new element properties, and a length of animation interval. For example, series orders for an element at position A like:
MoveTo(pos(B), 200ms);
MoveTo(pos(C), 200ms);
ResizeTo(size(C), 200ms); A 200ms animation of frames will be automatically generated with actual track path of transparent circles shown below:
Frames and sprites (the way element is called in graphic engine) are internal information maintained by graphic engine. Calling party only need to order script command as above and animated frames will be generated and attached to sprite. Besides MoveTo and ResizeTo, it also support transparency animation command FadeTo. Therefore, the rendered picture is easily brought alive with series of command.
GeneNode
GeneNode is a GUI interface of MetaIsland that works as a peer node in our parallel distributed network, an example screenshot looks like:
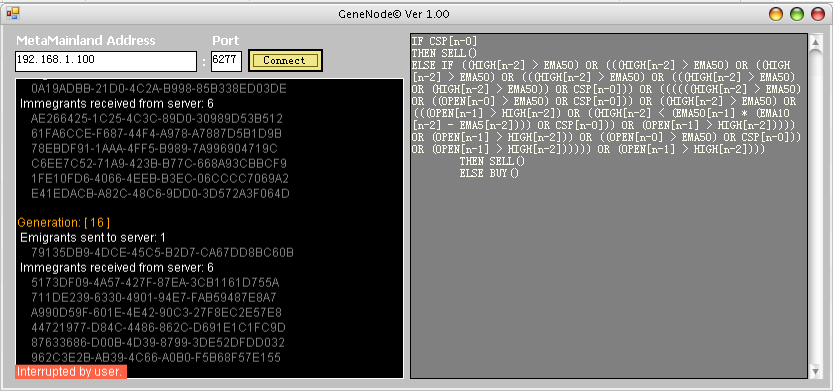
GeneNode has a very simple interface inherited from the simplified design of MetaIsland, although the mechanism behind involved a great amount of logics implemented on design models. The only input is server address and port. The text box on the left shows information as rolling text messages. We can see it just finished generation 16, one emigrant were sent to mainland, and 6 immigrants were received from other islands. Those strings are unique IDs of individual generated by system.
The text box on the right updates the current best individual’s program from last evaluation procedure.
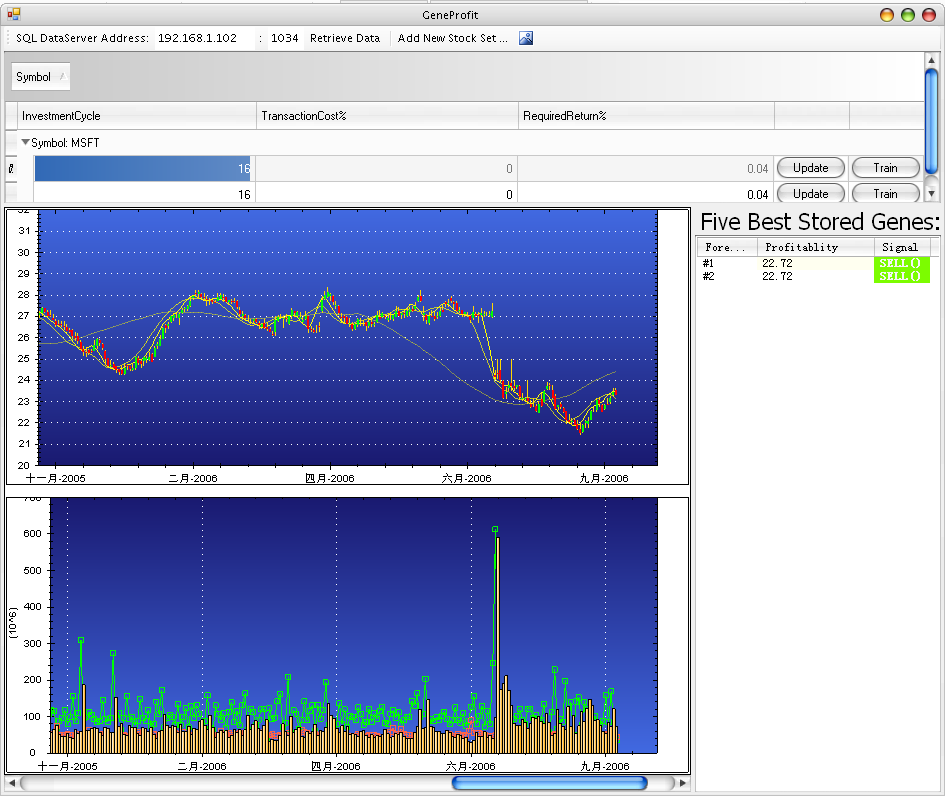
GeneProfit
GeneProfit is a control platform for financial market prediction. It also instantiates MetaMainland. The first screen showed to user is the stock management interface, where user can add/remove setting for stock predictions, either different sets for same stock or multiple stocks. Unlike other scientific programs, the interface of GeneProfit is kept very much simple. The vast logics of parallel distributed genetic programming are hidden from end user.
GeneProfit update information from Yahoo!™ Finance at background, historical data and statistical data calculated upon are then uploaded to Database. User can view the result of best stored strategy programs in Genebank for today’s stock ticker. User can also choose to train a particular setting, which will lead to train pane that actually instantiates MetaMainland and MetaGraphicEngine.
When user chooses to “Train” a strategy setting, the training setting window brought up:
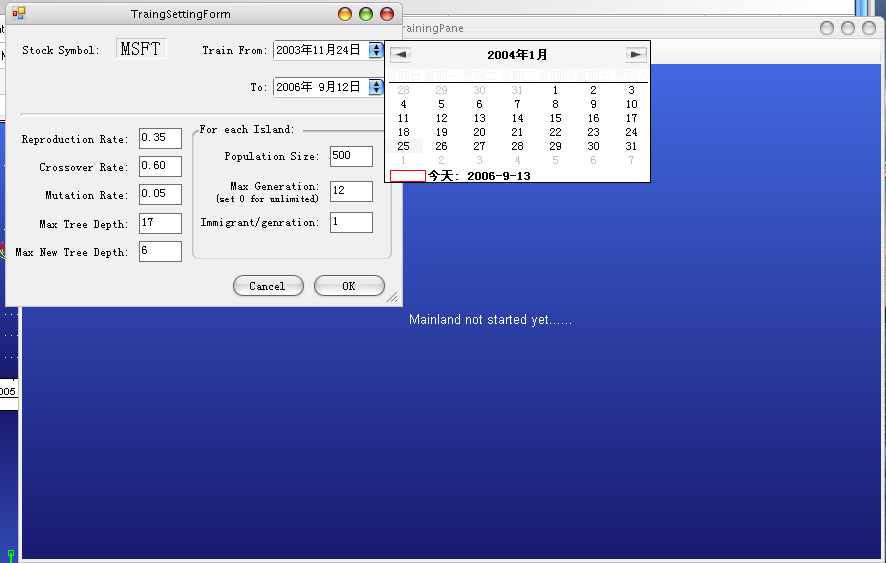
User can adjust basic parameter for genetic programming in this window, and start the training. Training can be applied on customized period of historical data. In this example, although Yahoo!™ Finance stores data for MSFT from year 1971, we choose to train individuals from year 2003 to now. Calendar format is customized by user’s operation system in this screenshot.
SQL Database
Conventionally, genetic programming implementations simply use text data files as input/output. This is a quick and easy solution. However, for a distributed cluster, and especially scale of this project, which involved large quantity of historical data and historical trained programs, local text files are the worst choice. But a solution is actually quite simple. All we need is a database system. Most modern database system supports distributed computing, and offers good performance on load balancing and access speed.
There are three tables in our design of database:
- Category: stores the settings for investment preferences.
- GeneBank: stores the individuals from each training process.
- FinancialData: one table per stock symbol. The historical data and technical statistics, only this table is accessible to islands in financial genetic programming.
Implementation
This chapter describes areas on implementation of this project, as a supplementary to most lacking details from previous chapters.
Programming Language and Development Environment
This project is chosen to be implemented by C# 2.0. A direct reason is that it is a good chance to learn this fast growingly popular programming language in software development industry. Secondly, dotNet framework offers an enormous but still very easy to use class library. Especially in socket programming, multi-threading, events and delegates, and GDI+ etc., these advantages are directly targeting at most elements of this project. Thirdly, the Visual Studio.Net developing environment is a very convenient and efficient IDE.
The SQL database system is chosen to be taken by Microsoft SQL Server Express 2005. Performance is needless to say for the scale of database used in this project. Firstly, it offers an industry leading graphical management tools. Building and configuring the whole database for this project is within a few clicks. Secondly, Visual Studio.Net IDE also fully support SQL Server. The coding for connections to SQL Server is also greatly simplified.
Genetic Programming
Generic Tree
C# 2.0 provides many new features on generic types like List, HashTable, Dcitionary, etc. But there is no tree type. In addition, even there exists one in C#’s library, we could not use it directly. Our genetic programming procedure requires extensive copy and cut operations on branches of trees. But the generic types provided in C# are actually by references, i.e., pointers. Therefore, a customized tree structure needs to be implemented for our project. And it is challenging to fulfil these features:
- It needs to support copy, cut, and paste of sub-trees.
- Tree nodes need to store object references as content.
- GeneNode
- MetaDGPEngine
- GeneProfit
- It should be able to quickly search for given object.
- It offers functionality to be serialised to XML strings, and also decode from a given XML string.
- It should use little memory and free up memory used quickly, since genetic operators development large quantities of new sub-trees quickly.
In our project, there is a complicated Tree structure implemented covering all above features in namespace MetaDGPEngine.Internal.Tree
Tree Creation Algorithm
Instead of commonly accepted GROW and FULL algorithms for tree-creation in genetic programming. This project adopts a newer and better Strongly-Typed Probabilistic Tree Creation (STPTC) (Luke, 2000). PTC is a modified version of GROW by employing probability of appearance of functions and variables in tree. Also tree size is well controlled in this algorithm. For financial genetic programming, we don’t want the strategy programs generated to be too long. This algorithm is modified to be strong typed according to the defined generic function nature in this project (next section on Action). The pseudocode of this algorithm is: (Luke, 2000)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Given:
maximum depth bound D
disjoint nonterminal subsets Ny of nonterminal set N for each yЄY
disjoint terminal subsets Ty of terminal set T for each yЄY
computed nonterminal-choice-probalilities py for each yЄY
For each Ty and Ny
Probabilities qn,y and qt,y for each tyЄTy and nyЄNy
Return type for the tree yrЄY
Do:
New tree T = STPTC(0, yr)
STPTC(depth d, return type yЄY)
Returns: a tree of depth <= D-d and of type y
IF d=D, return a random terminal from Ty (by qt,y possibility)
ELSE IF, with probability py a nonterminal must be picked,
Choose a non terminal ny from Ny (by qn,y possibilities)
For each argument a of ny of argument type ya
Fill a with STPTC(d+1, ya)
Return the completed nonterminal ny with filled arguments
Else return a terminal from Ty(by qt,y probabilities)
Binary Tournament Selection Method
The algorithm for selection in genetic programming in this project is Binary Tournament Selection (Koza, 1995). Each time two individuals are randomly selected, the one with higher fitness value will be selected into mating pool. This mimics the process of natural competition. And also guarantees that a super fit individual is not overly cloned in new generation. Hence loose the convergence of process of genetic programming.
Crossover and Mutation in Chromosome
The way how crossover and mutation works in this project is exactly as illustrated in background chapter. Crossover and mutation is implemented as public method in Chromosome class rather than individual, because Individual in MetaDGPEngine can incorporate more than one chromosome. This was due to that in some circumstances, for instance another design of forecasters in financial market prediction, an individual could have short-term, mid-term and long-term chromosomes as a fully capable forecaster.
There is a specially PickNonterminalRate by default set to 90% so that genetic operators tend to apply on inner trunk of trees.
Mersenne Twister Random Generator
An important element of Genetic Programming implementation is randomicity, which is fundamental to various aspects such as search space and selection process. However, in terms of implementation, most researches lose sight of the random generator provided by programming language. Although .Net framework is still new technology, the random generator it included in library implements a nearly 40 years old fluffy algorithm! This problem is similar to Java as well. Hence the system’s random generator set its own bias for our Genetic Programming implementation. Due to the enormous frequency that random number is used, this problem is never small to neglect. Therefore, in this project, I have adopted Mersenne Twister as our random generation, after researches and comparisons over many existing algorithms on efficiency and quality.
“The Mersenne twister is a pseudorandom number generator developed in 1997 by Makoto Matsumoto and Takuji Nishimura. It can provide fast generation of very high quality pseudorandom numbers, having been designed specifically to rectify many of the flaws found in older algorithms.” (Wikipedia)
This algorithm was designed to have a colossal period of 219937 − 1 (the creators of the algorithm proved this property). This period explains the origin of the name: it is a Mersenne prime, and some of the guarantees of the algorithm depend on internal use of Mersenne primes. In practice, there is little reason to use larger ones, as most applications do not require 2^19937 unique combinations. For example, to guarantee a completely random deck of cards only requires 52! combinations - approximately 2^225. Second, it has a very high order of dimensional equidistribution. By default, there is negligible serial correlation between successive values in the output sequence.
It is faster than all but the most statistically unsound generators. Quality is also guaranteed since it passes numerous tests for statistical randomness, including the stringent Diehard tests.
Pseudocode:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// Create a length 624 array to store the state of the generator
var int[0..623] MT
var int y
// Initialise the generator from a seed
function initialiseGenerator ( 32-bit int seed ) {
MT[0] := seed
for i from 1 to 623 { // loop over each other element
MT[i] := last_32bits_of((69069 * MT[i-1]) + 1)
}
}
// Generate an array of 624 untempered numbers
function generateNumbers() {
for i from 0 to 622 {
y := 32nd_bit_of(MT[i]) + last_31bits_of(MT[i+1])
if y even {
MT[i] := MT[(i + 397) % 624] bitwise_xor (right_shift_by_1_bit(y))
} else if y odd {
MT[i] := MT[(i + 397) % 624] bitwise_xor (right_shift_by_1_bit(y)) bitwise_xor (2567483615)
}
}
y := 32nd_bit_of(MT[623]) + last_31bits_of(MT[0])
if y even {
MT[623] := MT[396] bitwise_xor (right_shift_by_1_bit(y))
} else if y odd {
MT[623] := MT[396] bitwise_xor (right_shift_by_1_bit(y)) bitwise_xor (2567483615)
}
}
// Extract a tempered pseudorandom number based on the i-th value
function extractNumber(int i) {
y := MT[i]
y := y bitwise_xor (right_shift_by_11_bits(y))
y := y bitwise_xor (left_shift_by_7_bits(y) bitwise_and (2636928640))
y := y bitwise_xor (left_shift_by_15_bits(y) bitwise_and (4022730752))
y := y bitwise_xor (right_shift_by_18_bits(y))
return y
}
Late Binding via .Net Reflection
As described above, MetaDGPEngine is designed for generic purpose, not merely targeted at stock market prediction. It might be a lot easier for a single machine Genetic Programming implementation, but under a P2P environment things become much more complicated. We want our GeneNode to be a “thin” client, i.e. a “click-and-run” program without any configuration other than server address. This would greatly reduce the cost of maintenance, since all the modification and configuration for different problem or different parameters in same problem are only on server side. This is natural for Genetic Programming operators (selection, reproduction, crossover and mutation), because they do not care about the actual meaning of programs evolved. Problem comes from Evaluation process, where we need to access problem-specified data and functionalities. In a prototype version of this project, .Net Remoting was introduced. Those problem-specified data and methods are supported by remote calling server. However, soon we found out that Evaluation is the most time-consuming process, so this would completely slow down the whole performance and generate large overhead of network transactions, which eliminated any advantages on distributed computation. Therefore, we need a way to collection types and methods from server side and instantiate locally during runtime. Without reflection, this would be never made possible.
Reflection is an activity in computation that allows an object to have information about the structure and reason about its own computation. Reflective programming technique has been growing popular recent years. .Net’s industry leading reflection support is another reason C# is chosen. Many of the services available in .Net and exposed via c# depend on the presence of metadata. Reflection examines existing types via their metadata and is done using a rich set of types in the System.Reflection namespace. It is possible to dynamically create new types at runtime via the classes in the System.Reflection.Emit namespace, and/or extend the metadata for existing types with custom attributes. At runtime, these elements are all contained within an AppDomain.
Generic Type Converter
Parameters and variables are received from server as serialized hashtable, for example an integer describing MaxGenerations could be serialized as:
1
2
3
4
5
6
…
<MaxGenerations>
<Type>System.Int32</Type>
<Value>500</Value>
</MaxGenerations>
…
Upon received required variables, GeneNode need to create (instantiate) this variable according to its type, and then load the data by converting string to this particular type. We use Reflection to check if target type has a TypeConverter interface. A lot of non-basic types, including Unit, implement this because TypeConverter is also the way the designer in Visual Studio is able to use these types. If it doesn’t have a TypeConverter, try falling back to Convert.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Type propertyType = Type.GetType(node["Type"].InnerText);
string value = node["Value"].InnerText;
object convertedValue = null;
object[] attributes = propertyType.GetCustomAttributes(
typeof(System.ComponentModel.TypeConverterAttribute),
false);
foreach (System.ComponentModel.TypeConverterAttribute converterAttribute in attributes)
{
System.ComponentModel.TypeConverter converter =
(System.ComponentModel.TypeConverter)Activator.CreateInstance(
Type.GetType(converterAttribute.ConverterTypeName));
if (converter.CanConvertFrom(value.GetType()))
{
convertedValue = converter.ConvertFrom(value);
break;
}
}
if (convertedValue == null)
{
try
{
convertedValue = Convert.ChangeType(value, propertyType);
}
catch (InvalidCastException)
{
Console.WriteLine("Can't convert");
}
}
MetaTCPSocket Components
In design chapter we have listed the rationale of choosing a TCP protocol as the fundamental network communication layer for our distributed network. The parties communicating via TCP socket can live on different machines on the network, but they can also live on the same machine, or even within the same process. C# has a sound class in System.Net library called Socket that does most of the jobs.
However, it is still far from a finished encapsulated helper class to be used in this project. We need to implement a Server side and a Client side socket class for our mainland-island TCP communication. And further for a network service that is scalable and fault tolerance, we need to replace the threadpool provided in .Net library.
MetaTCPSocket namespace contains sealed classes trying to provide an all-in-one solution to the need of fast and reliable TCP client/server communications. MetaTCPClient implements the socket logics for client side, MetaTCPServer does the server side. MetaTCPClient is a very straightforward wrapper of Socket class with little added features like string form datagram. This is because that a client only needs to connect to one server, and clients usually expect to be blocked while waiting for information coming from server side. However, for a server side component, careful designs need to be done to ensure a bunch of features. Socket programming has always been mentioned as disaster since in network environment, nothing is impossible; and impossible come from no where.
- Scalability
A server side socket component needs to be implemented in the way of multi-threading. Therefore communication requests from different clients can all be served. We do not want to lose any incoming request, so each request need to be served in its own thread. Therefore, we need a mechanism to management this collection of threads.
- Load Balance
Since this parallel distributed genetic programming system is designed mainly for time-consuming computation tasks. Most of the time clients should be doing its own calculations. Therefore the network traffic is not very much significant. Therefore, server side socket merely adds a small delay to avoid DoS attack. Provided that our system is runned in intranet, there is little chance to be attacked in this form, so this feature is only added to prevent certain kind of faulty client.
- Fault Tolerance
Server needs to provide a high degree of fault tolerance and this feature needs to be transparent from user. The most significant problem is thread-safe. All communication requests are processed in separate thread. We need to check if the connection is already bad, so we can disconnect it and recycle the resources occupied.
Conclusion
Achievements
In this project, a working comprehensive software package is implemented that accomplished three main categories of challenges: parallel distributed Genetic Programming engine, financial stock market prediction, and a visualised distributed network interface. Many researches have been done to support rationales behind each category. I have learned a lot from each topic as well as developed own models where necessary. This project meets and beyond its initial specifications in many ways. Firstly, a generic Distributed Genetic Programming engine is developed, which can be applied to other problems rather than stock market for this project. Secondly, a financial genetic programming with various improvements to current research in this area has been achieved. This project suggests a new way to measure fitness value for financial activity is derived, and has its own approach on choosing technical indicators. Thirdly, a favourable graphic engine with frames animation is developed, which can be taken out as a separate component to be re-used in future project in other areas. Finally, this project presents a complete solution brings all these features together – GeneProfit.
Future Improvements
Due to the scale of this project, this project can be further improved from wide perspectives.
-
The distributed genetic programming engine can be evolved to a P2P system over internet. This requires a more reliable server, or may be clusters, to serve computing power from computers all over the world. Also, server side needs to have an improved security system.
-
The stock market prediction genetic programming system may be extended to other financial assets’ prediction. Or in another direction, the system could be redesigned to suggest hourly investment signals.
-
The end user interface can be further developed to be more human-friendly. For example, GeneProfit could automate task that update financial data everyday and train gene strategy accordingly. GeneProfit may be extended to be able to suggest portfolio combinations depending on forecast results. Or rather, GeneProfit can incorporate other means of financial prediction algorithm, for example, news sensitive prediction to overcome the disadvantage of purely based on technical analysis.
-
The visualised system can be greatly improved as well. Currently it does a great job to visualise and do basic management of distributed system. We could improve it as a visualised genetic programming solver, which allows user to create new problems visually and let the distributed genetic programming engine to solve customized problems.
References
- Alba E. and Troya J.M., A Survey of Parallel Distributed Genetic Algorithms, John Wiley & Sons, Inc. Vol 4, No. 4, 1999
- D.E. Goldberg, Sizing populations for serial and parallel genetic algorithms. Proceeding of the 3rd ICGA. Morgan Kaufmann, 1989
- Ehrentreich, A Corrected Version of the Santa Fe Institure Artificial Stock Market Model, University of Halle-Wittenberg, 2002
- Flynn, M.J. Some computer organizations and their effectiveness, IEEE Transactions on Coputers 21, 9, 948-960, 1972
- Iba H. and Sasaki T., Using Genetic Programming to Predict Financial Data, the University of Tokyo, 1999
- Jensen, M., Some anomalous evidence regarding market efficiency, Journal of Financial Economics, 6, 95-101, 1978
- J.H. Holland, Adaptation in natural and artificial systems, University of Michigan Press, Ann Arbor, 1975
- Kaboudan, M.A., Genetic Programming Prediction of Stock Prices, Computational Economics, 16: 207-236, 2000
- K.E. Kinnear, Jr., Advances in Genetic Programming. MIT Press, 1994
- Koza, J.R., Genetic Programming: on the programming of computers by means of natural selection. MIT Press, 1992
- Koza, J., Goldberg, D.Fogel, D. & Riolo, R. (ed.), Procedings of the Frst Annual Coference on Genetic Programming, MIT Press, 1996
- LeBaron, B., Building the Santa Fe Artificial Stock market. Working paper, http://people.brandeis.edu/blebaron/wps/sfisum.pdf. 2002
- Li and Tsang, Improving Techincal Analyusis Predictions: An Application of Genetic Programming, Florida AI Research Symposium, USA, 1999
- Luke, S., Two Fast Tree-Creation Algorithms for Genetic Programming, IEEE Transactions on Evolutionary Computation, 2000
- Montana, D.J., Strongly Typed Genetic Programming, Evolutionary Computation, 3(2):199-230. Cambridge, MA: MIT Press, 1995 M. Matsumoto and T. Nishimura, Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator, ACM Trans. on Modeling and Computer Simulations, 1998.
- Mayr, N., Animal Species and Evolution, University Press, 1963
- Miller, B.L. & Goldberg, D.E., Genetic Alorithms, tournament selection, and the effects of Noise, IlliGAL Report No. 95006, 1995
- Pictet O.V., Parallel Genetic Programming and its application to trading model induction, CUI, University of Geneva, 1997
- Sian, C. F., A java based distributed approach to Genetic Programming on the Internet, University of Birmingham, 1999
- Schoder, D. and Fishchbach, K. Peer-to-Peer prospects, Commun, ACM 46, 2, 27-29, Feb. 2003
- Tan K.C., Wang M.L. and Peng W., A P2P Genetic Algorithm Environment for the Internet, ACM 0001-0782, 2005 Potvin, Soriano and Vallee, Generation trading rules on the stock markets with genetic programming, Computers & Operations Research 31 (2004) 1. 1003-1047, 2004 Tanese, R. Distributed genetic algorithms. In Schaffer, J., editor, Proceedings of the Third International Conference on Genetic Algorithms, 1. pages 434–439, 1989